
Drag Efficiency in Rowing
In a recent article we’ve looked at the various aspects of defining and improving Efficiency in Rowing. In this article I want to expand on the concept of “drag efficiency” outlined in this article and how we can operationalize this concept for daily training to accurately asses a crew’s rowing technique. This article is guided by a simple question: How much faster can we go if we reduce velocity variation using efficient rowing technique?
Checking the Boat
It is an age old idea in rowing that “checking the boat” is counterproductive to efficient rowing. “Check” refers to the variation in shell velocity throughout the rowing stroke cycle and is most visible around the catch, which is ultimately caused by the periodic nature of the rowing stroke with a propulsive phase and a recovery phase.
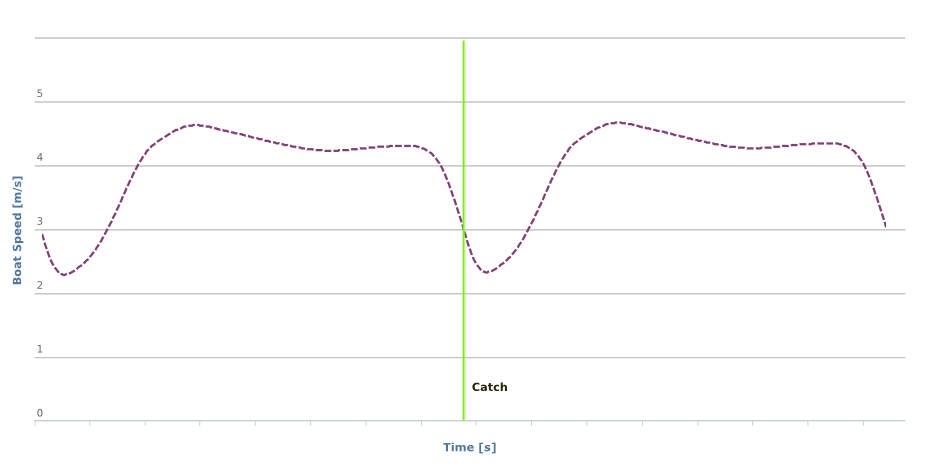
Variation of boat speed for two stroke cycles at 20spm.
The physics involved in rowing implies that the most efficient way to move a boat through the water is at a constant velocity. I’ll demonstrate this in the next section using an example, but for now let’s work with the implication that the amount of energy required to overcome drag (friction between the shell and the water) is minimal when the boat moves at a constant velocity. Any variation in velocity throughout the stroke will require additional mechanic energy to overcome drag, albeit achieving the same average velocity when looking at the full stroke cycle. Since the mechanic energy a crew can generate during a race is limited by physiological constraints, we need to minimize energy wasted on overcoming drag caused by velocity variation.
Unfortunately, it is impossible to avoid velocity variation of the shell during the stroke cycle. When we talk about winning races, the winning crew is the one that moves their boat down the track the fastest. But they don’t just need to move the boat, they need to move the whole system consisting of the boat, the crew and the oars down the track. In the propulsive phase of the stroke, energy is added to the system with the oars applying force on the pin and propelling the boat forwards. The system velocity thus increases during the drive phase. In the recovery phase however, system velocity decreases as it looses energy due to drag.
On top of this system velocity variation, we need to consider that the crew and the boat move relative to each other as well. Consider the crew sitting at the finish, just after extracting the blades: in this position all parts of the system move at the same velocity. However, as soon as the crew starts moving towards the stern of the boat to take the next stroke, the crew will move a little slower towards the finish line and the boat quite a bit faster. The boat and the crew exchange momentum and because the crew is much heavier than the boat, the effect on crew velocity is small while the effect on boat velocity is much larger (see “Momentum in Rowing” in the Efficiency in Rowing article for details). This leads to a very interesting effect: shell velocity varies much more than system velocity and the key to controlling it is carefully managing how the crew moves relative to the boat.
Before we go into these practical considerations, lets first look at the effect velocity variation has on boat speed.
Velocity Variation and Drag
You can safely skip this section if formulas and a bit of math are not your thing, just make sure to come back to the next section for the results and implications
First, we need to understand drag. The primary source of drag in rowing is fluid drag against the hull. In a simplified model that ignores unsteady effects such as surge, pitch etc., the drag force $F_d$ attacking the hull is proportional to the square of boat velocity $v$ and a hull-specific drag constant $c$.
$$F_d = c * v^2 \tag{1}$$
Because velocity varies over time, drag force is a function of time as well.
$$F_d(t) = c * v(t)^2 \tag{1.1}$$
Mechanic work is the energy required to move an object and calculated as the product of force applied and distance moved. Since the time-integral of velocity is distance, we can calculate the mechanic work (energy) required to overcome drag for a single stroke as the time-integral of drag force $F_d$ times velocity $v(t)$:
$$W_{d} = \int_{t_i}^{t_{i+1}}F_{d}(t) * v(t) \mathrm{d}t \tag{2} $$
Total work required to overcome fluid drag is minimal when velocity is constant and in this case simplifies to
$$W_{min} = c * v ^3 * (t_{i+1} – t_{i})\tag{3}$$
Using data captured about the boat, we can now take a look at the actual velocity variation during the stroke and the achieved average velocity to calculate the drag efficiency as the ratio of work required to overcome drag at the average velocity to the actual work required to overcome drag given the measured velocity variation:
$$\eta_{d} = \frac{W _{min}}{W _{d}}\tag{4} $$
One of the nice properties of this definition is that we don’t need to know the actual drag coefficient $c$ of the hull as it cancels out in the model. However, we need to know the actual velocity of the boat in the water and since drag efficiency defined in this way is a ratio of total energy required to overcome drag at that speed, it is highly dependent on average boat speed as well: Consider the effects of a given velocity variation (e.g. +1m/s in the first half of the stroke, -1/ms in the second half of the stroke) at an average velocity of 1/ms and 10m/s. The ratio will be much smaller in the first than in the second case, because at higher velocities the energy expenditure for overcoming drag will be much higher and the variation has much smaller weight.
Operationalizing Drag Efficiency
So as we’ve seen in the previous section drag efficiency is a useful definition that gives us the ratio of energy necessary to overcome drag given a constant vs. the energy required to overcome drag with the actual velocity variation. If e.g. you have a drag efficiency of 95% this means 5% of propulsive energy was wasted due to velocity variations.
Measuring the true drag efficiency requires accurate measurement of speed in the water and is highly dependent on the overall speed that a crew achieves, which is in turn dependent on environmental conditions and the propulsive energy generated by the crew. This will make it difficult to compare results in its current form between different crews and data recorded in different conditions. (For a general discussion of this topic see Using Measurements in Rowing.)
What we really want is a metric that measures the impact of a crews rowing technique on efficiency in a comparable way. What we can thus do is to take the actually measured velocity variation and superimpose this on a model that assumes the boat is moving at an average speed of $v=5m/s$, which is in the ballpark of a realistic 2k speed for a 1x/2- (6:40min). This solves two problems:
- we don’t need to know true in-water velocity, velocity above ground is enough
- results are comparable between different boats and crews, they’re a fingerprint of the crew’s stroke
We call this metric relative drag efficiency and you can work with it in the new Rowing in Motion App version 4.4 and later (see release announcement).
Improving Drag Efficiency
What can be saved
Before we look into specific aspects of rowing technique that improve drag efficiency, let’s first look at how much can be saved by rowing more efficiently. Using the definition of relative drag efficiency, crews typically achieve an efficiency between 89% and 98%, with efficiency generally decreasing towards higher stroke-rates and increasing for larger boat classes. This also intuitively matches expectations because higher stroke-rates require more acceleration on the slide and consequently more momentum exchange between crew and boat, resulting in higher velocity variations. A more “equal” weight relation between crew and boat in smaller boat classes (or lightweight boats) for example also results in less variation of boat velocity and consequently higher efficiency numbers.
I’ll spare you the math this time (have a look at the discussion in our forum for the model), but using the model of relative drag efficiency and solving for velocity we can actually calculate the seconds saved on a 2k race by increasing drag efficiency. This is working under the assumption of course that the crew goes at a 6:40min with its current rowing technique. Running all the numbers, we can say that an increase of 1% in drag efficiency will net you a ~1.4s advantage over a 2k race, at the same rowing power!
This might not appear to be a lot on paper, but considering this is true free speed and amounts to a full boat-length for a single at the finish line, it’s quite a substantial gain.
What works
Based on consultations with coaches working with junior rowers as well as elite teams preparing for the olympics we found that differences in relative drag efficiency between crews are typically smaller at the top (elite, 0.2-0.5%) than at junior or collegiate levels, where we found differences of up to 2% between crews of same age and boat class.
Leading rowing biomechanics expert Dr. Valery Kleshnev has addressed variation of boat velocity in issue #166 of his Rowing Biomechanic Newsletter and compiled the following recommendations that I wholeheartedly agree with:
- Avoid sharp jerky pulls of the stretcher during recovery: Try to spread stretcher pulling force evenly to produce the most constant boat speed and minimise energy losses.
- Use optimal gearing ratio according to weather conditions: shorter outboard at head wind. Avoid too heavy gearing, which makes drive too slow and requires rushing on recovery to maintain the stroke rate. Shorter recovery time requires harder pulling the stretcher, which accelerates the boat more and increases variation of its velocity.
- For the same reason, do not put the blade too deep during the drive, which may “break the force curve” and make drive time longer.
- “Front-loaded” drive with quick force increase after catch is the only way to accelerate the boat earlier during the drive and make its velocity more even.
For a visual explanation of these concepts, I suggest you read Optimize Your Rowing Stroke with Rowing in Motion. Even if you haven’t worked with Rowing in Motion yet, it doesn’t hurt though to take a look at an example. Both crews shown in the figure below have different “issues” in their signature stroke’s boat acceleration. What’s interesting about drag efficiency is that it gives you a singular number that weights the impact of all these different aspects using a sound physical model.
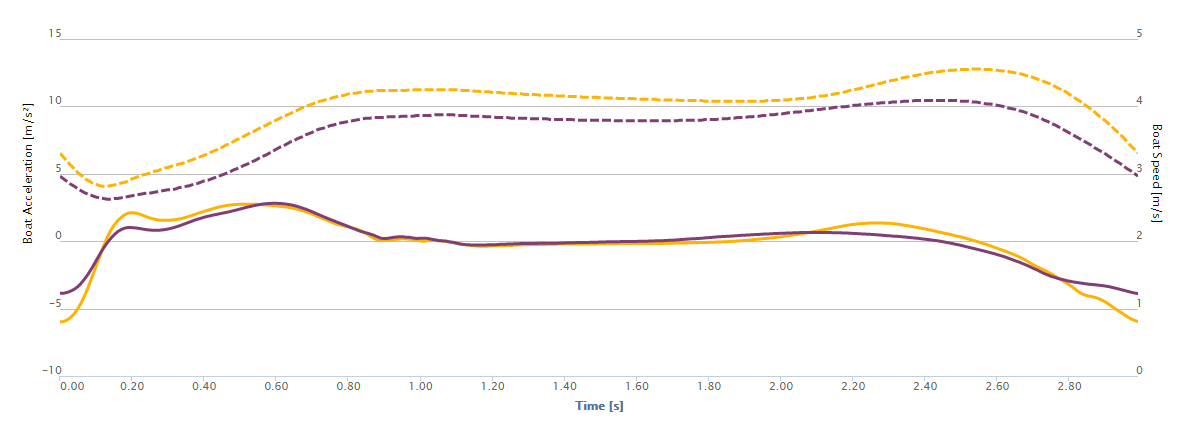
Two Junior Eights at SF20. Relative drag efficiency yellow: 97.6%, purple: 97.9%
These are two junior eights at steady state stroke rate. We can clearly see that the yellow boat has a better catch duration (470ms) than the purple crew (520ms), however the yellow crew actively accelerates the boat on the slide before the catch by pulling forcefully on the stretcher. This creates an unnecessary variation in boat velocity, offsetting their much better catch and drive phase.
What doesn’t work
Many things have been tried to improve drag efficiency in the history of rowing, one of the more obvious ones being “Syncopated Rowing”, where the crew rows asynchronously to ensure constant propulsion of the boat[1]:
There’s a variety of reasons this didn’t work very well. Chief among them is that this style of rowing very difficult for the crew to perform and that the crew members need to expend additional energy to overcome inertia forces when they move “against” the boat.
There’s also been sliding riggers, which reduce the mass moving relative to the boat (the rigger moves, not the crew) and have a few other advantages because they reduce surge and heave of the shell. Unfortunately, they have been forbidden.
And then there’s a few obvious other things you can try to cheat yourself into rowing more efficiently. See that acceleration during the drive phase? Well, this is actually not that efficient either since every acceleration of the boat results in variation of boat velocity, right? You could try pulling less harder, it will increase efficiency. This is obviously a red-herring. Rowing more efficiently at less power is certainly not going to make your boat go faster. Efficiency is thus not the end-goal of all rowing, we also need to set up the crew with a rowing technique that allows it to generate the maximum propulsive energy that it is capable of.
Footnotes:
[1] See this Rowing News article by Volker Nolte for a nice review of the history of Syncopated Rowing.
There’s some recent research on syncopated rowing http://www.ncbi.nlm.nih.gov/pubmed/23383024 that also shows the potential for a 5-6% gain.
Another way to assess rowing efficiency is to use the concept2 weight adjustment calculator. I average the weight adjusted erg scores for the rowers in the shell, then apply a boat efficiency multiplier, and that tells me how fast that crew should be able row. Have to test in a no-wind condition. Yes, 100% is achievable.
Weight adjusting erg scores is generally a good idea, though the exact formula to use is highly debatable. Good empirical validation is often lacking…. In any case, ergs don’t float!
Yes, finally. Someone mention the obvious. I am fed up of hearing about giving the boat the smoothest ride, as if the crew weight and water vs wind resistance doesn’t matter.
What I would be interested in, is to see Rowing in Motions thoughts about the difference in boat angle in the catch and how it affects the boat speed. Kleshnev is consistent in saying the power needs to be applied _before_ entering the water with the blades. This would check the boat a bit more than tricking the blades in without power (but then again introducing a stopping motion before power and also loosing some of the range of motion). How much will the added stern dip add to the drag of the boat?
This is a very interesting question – and it depends on a lot of factors. I can highly recommend Leo’s FIRM rowing model that can answer these questions very exactly for your particular crew and your particular boat: http://www.boatdesign.net/forums/design-software/free-internet-rowing-model-2-32-released-52866.html The manual has a great and accurate description of rowing physics as well. Mind you, it’s quite a complex piece of software (due to the complexity of the math).