Efficiency in Rowing
In this article I want to look at possible definitions of efficiency in rowing and what makes a certain rowing technique more efficient than another one. The term “Efficiency” always describes a ratio of two factors, typically in an input to output relationship.
What are those output and input factors in rowing? When we look at the optimisation of rowing technique with the goal of moving the boat over the finish line as fast as possible in a race, our output is the average boat velocity. The average boat velocity $v_b$ is defined by the ratio of race distance and the time it takes to move our boat from start finish.
$$ v_b = \frac{d_{total}}{t_{total}} \tag{1.1}$$
$$=> d_{total} = v_b * t_{total} \tag{1.2}$$
What input is required to move a rowing boat down the race course? This is where things get interesting and commonly used definitions of efficiency in rowing diverge.
Mechanic Efficiency
Let’s look at the mechanics of rowing. The challenge for the crew in rowing is to move the boat through fluid water and through air by means of a periodic propulsion with the oar-blades. If we simplify a little bit and look at it only in the horizontal direction, the crew is connected to the boat through the stretcher which is affixed to the hull. Hence, the crew doesn’t only have to move the boat but the whole system consisting of boat, crew and oars down the course.
The crew + boat + oars system has only a single point of exchange of propulsive forces (that is forces that move the system forwards) with the outside world: the oars. If we look at it from high-level perspective, the ultimate metric for mechanic efficiency is the ratio of mechanic work input on the handle in relation to the achieved average boat speed.
$$=> \eta_{mechanic} = \frac{v_b }{W_handle}\tag{1.3}$$
This metric however overlooks the important details of where exactly any inefficiencies come from. It doesn’t tell us what we can improve to row more efficiently. Thus, let’s look at some of the most important sources of mechanic inefficiency.
Propulsive Efficiency
The propulsive efficiency of the blades defined as the ratio of propulsive work vs. to the work input on the handles deserves an article on its own and could fill books.
The bottom line is, that blades do not translate all the mechanic energy put into them via the handles into increased kinetic energy of the rower+boat+oars system, but some of it is lost in the “puddle” – you make water swirl which some may find looks nice, but it doesn’t move the boat. The propulsive efficiency of the blades does however not only depends on the blade shape, rigging and blade work of the crew. A key part is that the blade efficiency changes throughout the drive and it thus matters when and how much force the crew applies. Contrary to common belief, the blades are not the most efficient when their angle is perpendicular to the boat’s centreline, so a correct sequence of force applications is important to achieve maximum propulsive efficiency.
Fluid Drag Efficiency
When this system moves through water, it experiences friction generating a drag force against the direction of movement. The primary source of drag in rowing is fluid drag against the hull. The drag force $F_d$ attacking the hull is proportional to the square of boat velocity $v_b$ and some hull-specific drag constant $c$ (this is of course a slight simplification, in real life hull-drag is a function of many different factors such as speed , orientation of the hull, water temperature…):
$$ F_d = c * v_b^2 \tag{2}$$
The crew needs to overcome this drag force while moving the boat along the total distance $d_{total}$. The mechanic work to be accomplished by the crew in a race is thus:
$$W_{total} = F_d * d_{total} \tag{3} $$
There’s one inaccuracy in equation $(3)$ above though: The boat does not move with constant velocity. In fact, the boat is subject to various forces and the resulting total boat force accelerates and slows down the hull in a cyclic pattern throughout the stroke.
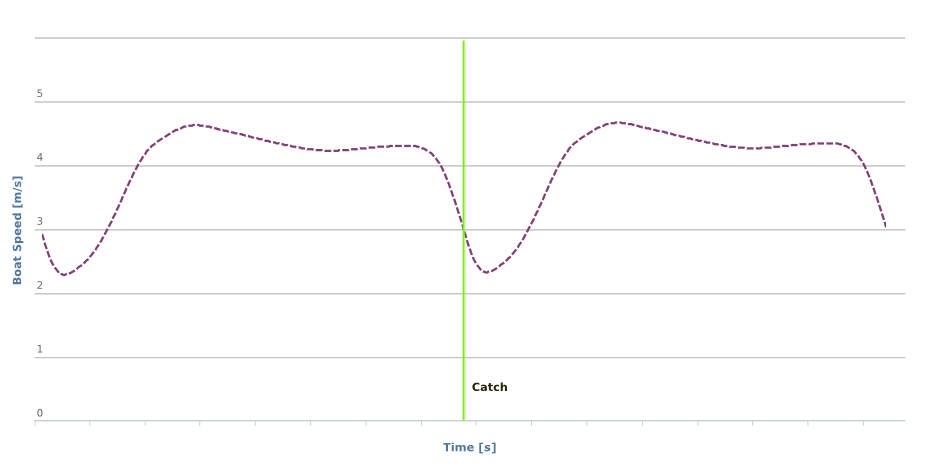
Fig. 1: Variation of boat speed for two stroke cycles at 20spm, measured with the Rowing in Motion System.
These forces are in particular stretcher force, gate force and the drag forces acting on the hull. For the total work required to overcome fluid drag, this is very important because the work is proportional to the cube(!) of boat velocity. Let’s derive this by substituting $(1.2)$ and $(2)$ in equation $(3)$.
$$ W _{total} = F_d * d_{total} = c * v_b^2 * v_b * t_{total} = c * v_b^3 * t_{total} \tag{3.1} $$
The cubic relation to boat velocity has an important practical consequence for rowers: The mechanic work required to overcome fluid drag is minimal when the boat moves at constant velocity. This article is not intended to be read by mathematicians, so I’ll spare you the proof and show you an example instead that will illustrate this concept. Say the boat should move at an average velocity $v_b = 5m/s$ and thus needs 400s to cover a distance of 2000m. The total work required would thus be:
$$ W _{vconstant} = c * 5{m/s}^3 * 400s = 50.000 * c \tag{4.1} $$
If instead the boat moved at $v_{b1} = 4m/s$ for the first 200s and $v_{b2} = 6m/s$ for the second 200s, the average speed would still be $v_b = 5m/s$ but the total work required would be considerably larger:
$$ W _{vvariable} = c *(v_{b1}^3 * 200s + v_{b2}^3 * 200s ) = 56.000 * c \tag{4.2} $$
So as we can see in this simple example, controlling the variation of boat speed is important to minimize the mechanic efficiency in rowing. We will call the ratio of the efficient (= minimal) work to the actual work required by a boat to overcome fluid drag fluid-drag efficiency.
$$ \eta_{fluid-drag} = \frac{W _{vconstant}}{W _{vvariable}}\tag{5} $$
(The greek letter $\eta$ is pronounced “eta”). From this mechanic point of view focussing on fluid drag efficiency, controlling the variation of boat speed applies to the intra-cycle variations of boat speed (see Fig. 1) as well as the variation of average stroke-cycle boat speed during the race (“pacing strategy”). One nice property of this definition of fluid-drag efficiency is that the actual drag-coefficient of the hull is irrelevant and does not need to be known.
Air Drag Efficiency
The rower-boat-oars system experiences drag not only in the water (although this is a dominant factor) but also in the air, with the primary source of drag being the crew and the oars. You might be tempted to discard these as unimportant, but think about the margins that even the tiniest improvements in reducing total drag by 0.1% can bring you at the finish line: at $v_b=5ms$ this could be as much as $0.5s$!
Reducing the mechanic work required to overcome air-drag follows the same law as minimizing fluid-drag, we can thus define a similar air drag efficiency as the ratio of efficient (= minimal) work required to overcome air-drag to the actual work required to overcome air-drag in the face of velocity fluctuations.
There are two two important caveats however. First, we can actually change the drag coefficient of the crew $c_{crew}$ and the oars $c_{oars}$ for the stroke-cycle by means of an optimized motion sequence. This is different than for the hull, which has a more or less unchangeable drag coefficient. For example, a later squaring of the blades will result in a smaller drag-coefficient $c_oars$.
Second, we can again minimize the fluctuation of velocity of the crew and the shell relative to the air. While the air-drag of the shell and the attached riggers is minimal when the velocity fluctuations of the shell are minimal, our ability to minimize velocity fluctuations of the shell and the crew at the same time are quite limited. The primary reason for that is the relative movement of the crew on the sliding seats to the shell. We can describe this relative movement by the means of an exchange of momentum.
Momentum in Rowing
If we step back from our perspective on minimizing work spent on drag for a second and assume there was no drag whatsoever and the crew + boat system would move at a fixed velocity (which could be zero or anything else) with no relative movement of the crew towards the boat, then the system momentum $p_s$ is the product of system velocity $v_s$ and system mass $m_s$.
$$p_s = v_s * m_s \tag{6.1} $$
Because there are no drag forces in this thought-model, the crew and the boat could change their relative velocities and exchange momentum without changing the system’s momentum $p_s = const$ according to the law of Conservation of Momentum. Stretcher force is thus irrelevant for the system velocity, but very important for boat and crew velocity!
$$p_s = v_{boat} * m_{boat} + v_{crew} * m_{crew} \tag{6.2} $$
This momentum exchange happens whenever force is applied to the stretcher and is thus inevitable during the stroke cycle. (The contribution of blade force and the matching counter-force at the pin increases the system velocity and thus changes system momentum.) Because the crew and boat exchange momentum during the stroke-cycle, minimizing total drag as the sum of air-drag and fluid-drag is a multi-dimensional optimisation problem. In practice, this means that the optimal total drag efficiency will deviate from the best realistically achievable fluid and air-drag efficiency.
Things will get even more complex once we take into account the physiology of the crew.
Physiological Efficiency
The concept of mechanic work is fundamentally unintuitive to many rowers and coaches. Mechanic work is defined as the product of force and distance, or $W = F * d$. If you were to push against a concrete wall and the wall doesn’t move, this would certainly be exhausting. You would have also generated a significant force attacking the wall. From a mechanical point of view however, you have done no work – the wall didn’t move, or $ W = F * 0 = 0$.
What is the source of this common misconception? Oversimplifying the process, the human body converts chemically stored energy into force and heat. Lots of heat! When you push against the wall and it doesn’t move, you still need to expend energy to create the force to push against the wall. You have spent chemical energy and done no mechanic work for it, your efficiency is thus $0$. The wall on the other hand didn’t need to expend any energy to create a counter-force to your hands pushing against it. That’s because its molecular structure is rigid.
Metabolistic Efficiency
When we talk about physiological efficiency in rowing we need to look at the input of chemical work and the output of propulsive mechanical work. The “input” into this equation is indeed very difficult to measure and depends on many factors. One aspect for example that has been well researched is the effect of muscle contraction speed on force and consequently power production. It has been shown, that there exists an (individual!) optimum contraction speed so that the work performed by the muscle is maximal. One optimisation goal is thus employing the individual muscles in a motion sequence with a contraction speed that maximizes their ability to perform mechanic work.
Physiological Load Efficiency
Another important aspect of physiological efficiency is how much work the rowers organism performs during a race in relation to its theoretical (and this is hard to define!) maximum. This is for example one aspect where a pacing strategy comes in.
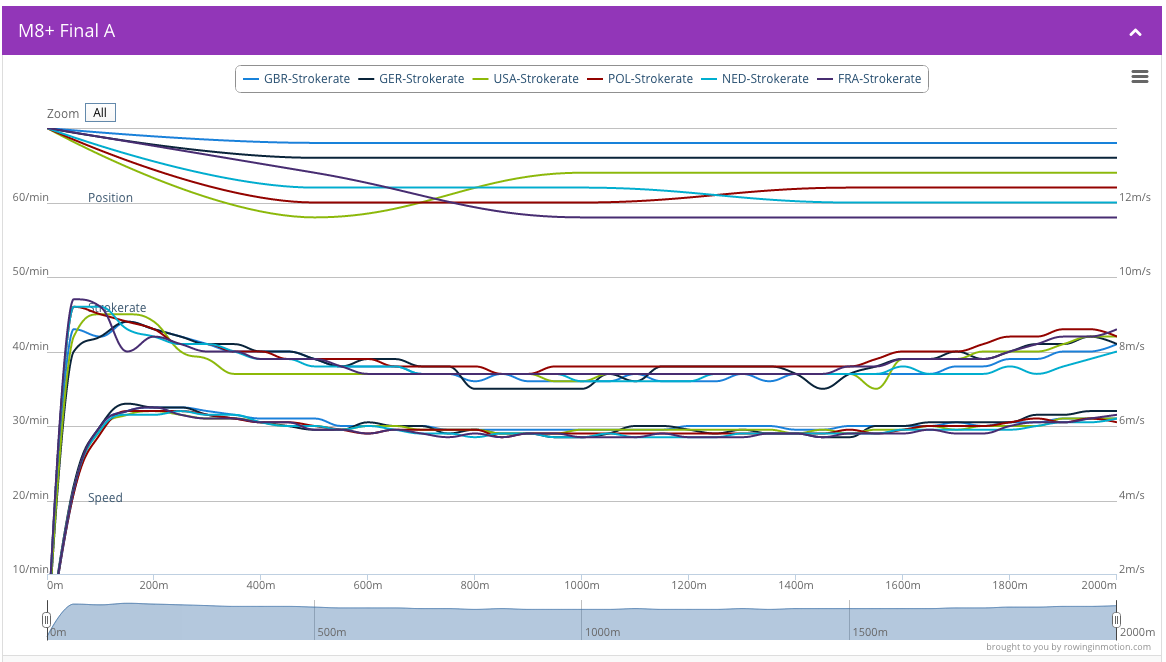
Boat Speed for the M8+ Final at the 2013 World Rowing Championships. Note that the curves have a distinct “bowel” shape with higher speeds at the start and finish.
A quick sprint at the start and throughout the first 500m that we can commonly observe at world cup races (e.g. the WC M8+ Final 2013 in our FISA Race Analyzer above) may be counterproductive from a fluid-drag efficiency point of view, but it maximizes an athletes ability to perform mechanical work with chemical energy provided by separate systems in the body (aerobic, anaerobic).
Rowing Efficiently
I hope this article has given you some insight into the aspects of what it means to row “efficiently”. Rowing is a very complex sport and optimising only a single aspect of it may be at the cost of total system efficiency and boat speed. Hence, careful measurement of the relevant performance parameters is required.
The physiological aspects of rowing have received much attention in research and important insights are applied in coaching today at all levels (i.e. lactate tests, heartrate monitoring etc.). Unfortunately, we can’t say the same about the mechanical aspects of the rowing stroke.
It is our vision to change that! Tools like Rowing in Motion effortlessly measure important aspects like the total propulsive force on the boat and the cyclic pattern of boat speed and can be applied by coaches and athletes on all levels.

As a relatively new recreational rower with an interest in science, this is fantastic. Something I’ll be sharing with my coaches for sure.
Can I ask who the author of this article is? I want to source them on a research paper I am writing about the physics of rowing, as it is so effectively explained here.
Sure, you can cite it as Johannes Rudolph, In Motion Software & Sports Technology GmbH. I’ll be glad to have a read through your paper when it’s done. You can reach out to me at johannes@rowinginmotion.com