Stroke Efficiency Explained
With metrics Rowing in Motion gives you some numeric information about typical strokes and allows you to compare typical strokes beyond the purely visual difference in a graph.
The calculations for the metrics are not a secret in any way and we’re happy to share the exact calculations we use. In fact, we believe it is very important that we are open about how we calculate these numbers so that people can review the calculations and make up their minds about the model and its values. If a little math scares you, I suggest you skip the next paragraph and go directly to the intuitive explanation below.
Calculating Stroke Efficiency
All our metrics are based on a typical stroke, which is simply a function $a(t)$ which produces the boat acceleration at time $t$. To simplify, we can define $a(t)$ as a function that combines $n$ strokes $a_1(t) … a_n(t)$ using the arithmetic average.
If $a(t)$ is the acceleration of a typical stroke at time $t$, then stroke efficiency $se$ is simply:
$$se = \iint{a(t)}\mathrm{d}t$$
With units, we go from m/s² to m, so stroke efficiency is actually a distance. However, this is not the distance per stroke since we integrate the changes in velocity (=acceleration) relative to the velocity v0 at the start of the stroke t0 to the then of the stroke t1.With this definition, distance per stroke is:
$$ d = (t_1 – t_0) * v_0 + \iint{a(t)}\mathrm{d}t $$
At this point, it’s also useful to define inter-stroke speed v, which is:
$$ v = d/(t_1-t_0) $$
On a sidenote, we currently do not provide distance per stroke metrics because the combination of smartphone gps and accelerometer is unable to achieve a desirable level of accuracy. Our upcoming Sensorbox can, down to an accuracy of a few cm.
The crux of the model for stroke efficiency is that we suppose that there is a “base speed” $v_0$ – the speed of the boat at the catch and we assume this is a given, constant speed that the boat moves with. If you think about it, this makes sense. There’s another invariant that should hold for each stroke when we move at a constant average speed and that is that $v(t_0) = v(t_1)$ (or else the boat would be getting faster/slower stroke by stroke). What we are now looking for is the deviations from this speed and how it helps cover “extra” distance on each stroke. Note that during the whole explanation we do intentionally say speed, not velocity as the double integration of boat integration yields a distance rather than a displacement!
Intuitive Explanation
Stroke efficiency is the distance covered each stroke due to the speed deviation from the speed of the boat at the catch.
Let’s make a small though experiment and suppose the crew is rowing on a river against a current with exactly the same speed as the boat has at the catch relative to the water and we’re observing it from a fixed point on the land. With this thought-model the boat would appear to stand still at the catch. Then we would actually see the boat reverse first (because the boat is decelerating) then accelerate again and cross the position it had at the catch.
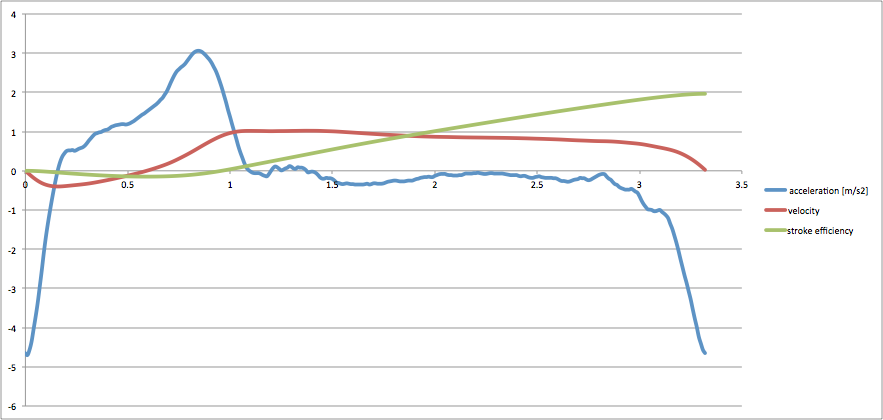
The diagram below shows the acceleration of the boat (blue), the relative velocity (red) and stroke efficiency (green). As you can see, this happens somewhere at the end of the stroke, around 1s in this diagram.
While you maintain a boat speed that exceeds the boat speed at the catch during the stroke, the boat accumulates “extra” distance (which we call stroke efficiency).
So what makes a stroke efficiency a good (or not so good) metric then?
It does reward gaining speed early in the stroke, and it rewards maintaining a high boat speed during the recovery (aka don’t piss of the boat). These are two traits that we have observed to be a common difference between excellent (international) and “normal” rowers (national and club level). The metric values we saw reported from crews in these two groups of rowers match this. (We’d be more than happy to support a proper study on this!)
You might ask why is gaining speed early in the stroke and maintaining it for longer positive? Well, if you’re faster for longer you have a higher intra-stroke speed (the average speed of a stroke). Would stroke efficiency also reward being extremely slow at the catch? Yes. And that’s why it’s not a “perfect” metric and you need to see the whole picture. But chances are that if the boat is extremely slow at the catch (and getting it back to speed requires a lot of energy) that you’re doing something wrong anyway.
Tying this into the physics of fluid dynamics on the shell (and what effect changing its speed during the stroke has and whether that means we want high vs. low stroke efficiency) is an interesting question, but that is beyond the scope of this article, but needless to say that there are some advantages to keeping fluctuations in boat speed to a minimum.
The least we can say about stroke efficiency is that it’s a useful metric to describe and compare different acceleration profiles. Stroke efficiency alone doesn’t tell you which profile is faster, that’s a question that we should decide on the regatta course. Rowing remains a multi-dimensional optimisation problem.

So, do I understand this correctly: all else being equal (stroke rate, power application, etc) stroke efficiency will be higher downstream vs upstream?
No, there shouldn’t be any difference. Stroke efficiency is relative to the inertial reference frame of the boat. If you think about it, it’s based on acceleration and while the boat is floating on the stream there will be zero acceleration due to the stream (as the boat is constantly moving with it).
The example I made about the stream that has the same speed as the boat has at the catch above was purely for visualisation purposes.
It is not a proper measure of efficiency, it appears to be a measure of work or power. The greater the variation in shell speed between catch and finish the slower the average speed. Also the velocity of the shell (the red line) should continue to rise after the finish as the body mass moves towards the stern.
James, thanks for your comment. It’s great to see that you’re thinking it through.
It’s neither work nor power (=the rate of work). Work is force x distance, but the unit of stroke efficiency is m. It’s really only the distance covered due to speed variation _relative to the speed at the catch_. Calling it stroke efficiency may have indeed been a bad choice on my part, as it isn’t an output/input ratio which the name suggests.
My original observation and thus intention of calling it that way was that faster crews tended to have higher values on this metric.
“The greater the variation in shell speed between catch and finish the slower the average speed”:
is a wrong conclusion. I can see where you are coming from though. It’s indeed useful to minimize speed variation during the stroke cycle as this will decrease the work required to cover a certain distance (this is actually what we should call something-efficiency). However, the boat is _slow_ at the catch and we want it to go fast. We increase average speed only by going fast for long (and conversely going slow for short). The variation in speed is natural due to the way rowing works as a cyclic sport that cannot generate a continuous propulsive force.
“Also the velocity of the shell (the red line) should continue to rise after the finish as the body mass moves towards the stern.”:
This is a question of the speed that the body mass moves with and is only related to the force applied on the stretcher (neglecting minor forces on the oars and sliding seat). If you pull hard on the stretcher with a force that is larger than boat drag force, you will indeed get faster in the recovery. This typically happens at higher stroke-rates (beyond 26spm from my experience), but not at lower strokerates like displayed. The answer to the shape of the speed graph is the acceleration graph, which again is shaped by the forces acting on the boat.
(A quick note: when you accelerate towards the catch e.g. as it happens at 26spm, this is no “free speed” – you need to push harder on the stretcher as a consequence when you want to turn around and this will make your boat slower by then. You can think of this as an impulse exchange between rower and boat. It is advantageous to maintain a “constant” pull on the stretcher as this will yield the flattest speed graph which has the best energetic efficiency. Also, muscles can generate more force when they contract slower which is another benefit of arriving with less speed on the slide at the catch, which should be quick and hard, yet smooth….)